Étienne Fouvry: Hunting for prime numbers
Étienne Fouvry, an Emeritus Professor at Université Paris-Saclay and member of the Orsay Mathematics Laboratory (LMO – Univ. Paris Saclay, CNRS), has dedicated his career to arithmetic and prime numbers. This enthusiastic mathematician is still fascinated by solving mathematical problems, some of which have remained unsolved for many hundreds of years. The French Academy of Sciences recently awarded him the ‘Sophie Germain - Fondation de l’Institut de France’ 2021 prize for his work.
Étienne Fouvry entered the ‘École Normale Supérieure’ (ENS) Ulm in 1972. With his passion for classical mathematics, he leaned towards analytical number theory, which was a relatively unfashionable field of study at the time. He was drawn in by the varied and particular structure of this area of mathematics - the result of a lengthy history - since some of the problems posed by ancient scientists were still befuddling mathematicians. “I was happy to be able to compare my ideas with those of people who lived so long ago,” reveals the researcher.
During his time as an assistant at Université de Bordeaux, in 1981, Étienne Fouvry defended his thesis about the distribution of prime numbers in major arithmetic progressions. Under the supervision of mathematicians Henryk Iwaniec and Jean-Marc Deshouillers, he focused on prime numbers - these whole numbers that can only be divided by themselves and by 1. The list of them, starting with 2, 3, 5, 7...is infinite. Nowadays, the researcher still feels just as much enthusiasm for this field of study: “Number theory is a remarkable field of research because of the clarity of resulting theorems but is also formidable because of the difficulty of the methods used. For example, I studied the behaviour of prime numbers in arithmetic progressions. This is a simple concept that defines numbers separated by the same interval, such as counting in fours from five.”
Arithmetic: a discipline that deserves to be shared
Étienne Fouvry was awarded the role of Professor at Université Paris-Sud (now Université Paris-Saclay). He split his time between research and his students. He feels lucky to have been able to teach and derived great pleasure and personal balance from it. He supervised eight theses and developed several European partnerships. For him, sharing is a core value. “I was lucky to work with such enthusiastic and passionate colleagues, who liked to exchange ideas and who took real pleasure in solving problems.” He explained the importance of collaboration between mathematicians: “The aim of a mathematics publication is to come to a true statement. Yet, if we miss the intermediate step, the whole statement falls apart. Working together allows us to overcome this problem. Publishing an article is like pole vaulting - if the bar is high but we can’t get over the obstacle, we won’t make history. If the bar is far too low, no one will be interested in the result. Only co-operation between several researchers can mean putting the bar up high and overcoming it.”
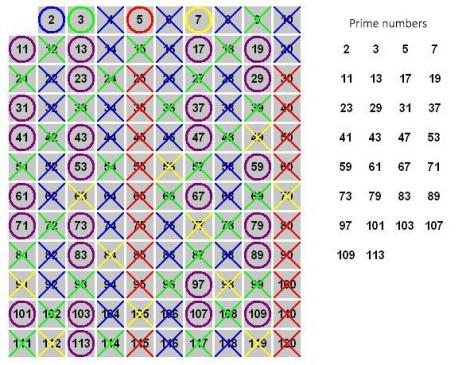
Looking for prime numbers
One of the main tools used by Étienne Fouvry in his work was sieve theory. The sieve of Eratosthenes, which is often studied in high school, is a simple example. To find the prime numbers between 1 and 100, we need to go through this number sequence in ascending order. Each new number we come across is noted down, and multiples are eliminated. We continue this process until the end of the grid. This sieve was developed during Classical Antiquity, but is no longer suitable for arithmetic today. Other, more efficient, sieves are needed. The development to which Étienne Fouvry dedicated his research.
Pioneering work that led the way
From the 1980s, Étienne Fouvry studied twin prime numbers, which are sets of numbers with a prime gap of two, such as 3 and 5, 5 and 7, 11 and 13, and so on. Like many other arithmeticians, he wanted to prove that infinity exists. He significantly contributed to this field, and his work was cited in Chinese mathematician Yitang Zhang’s pivotal article that proved that an infinity of prime numbers does exist if the difference is less than 7 · 107. One of his first pieces of work, which he presented in 1985, helped three other mathematicians develop the AKS primality test in 2002. Thanks to this test, we can now easily find out if a number is prime.
After 10 years of work on these major arithmetic progressions, the mathematician focused his research on a new path. “I was going in circles. Yet, I think that maths should be done with pleasure. You have to know when to change the subject and stay curious to never get bored.” In 1997, in collaboration with Henryk Iwaniec, he discovered a new infinite set of prime numbers. These are the ones that can be decomposed into a sum of the square of an integer and the square of a prime number. The first components of this sequence are therefore 5 = 12 + 22, 13 = 22 + 32, 29 = 22 + 52... They are now called Fouvry-Iwaniec prime numbers.
Subsequently, the mathematician made progress in understanding the negative Pell equation, written as x2 - dy2 = -1. It was developed using a problem dating back to the time of Archimedes and, depending on the value of ’d’, does not always have a solution. Étienne Fouvry succeeded in finding a large number of instances where the equation can be solved.
The Sophie Germain Prize and the long tradition of number theory
Recently, the French ‘Académie des Sciences’ chose to reward Étienne Fouvry’s work by awarding him the Sophie Germain Prize, named after a pioneer of 18th century arithmetic. “I am delighted to have received the prize that bears her name,” says Étienne Fouvry. This self-taught mathematician, who had to fight to assert herself in the scientific world of her time, left a legacy of a theorem on prime numbers and research in physics and philosophy.
Like Sophie Germain, Étienne Fouvry was interested in Fermat’s last theorem. Since the discovery in 1670 of the annotations left by the mathematician Pierre de Fermat in the margin of a book, this theorem has aroused much debate. “A cube is never the sum of two cubes, a fourth power is never the sum of two fourth powers, and more generally, no power greater than two is the sum of two analogous powers,” explains Étienne Fouvry. “I have discovered a wonderful proof, but the margin is too narrow to contain it.”
Generations of mathematicians have sought to prove the truth of this theorem for all instances, proceeding step by step and extending the proof to larger and larger sets of powers. Shortly after 1800, Sophie Germain made a significant contribution to the subject, which Étienne Fouvry built on in 1985 to push the issue further. In 1994, Andrew Wiles finally developed a complete proof.
Having retired three years ago, Étienne Fouvry is now Professor Emeritus. He is now interested in binary forms of any degree and in trace functions. He plans to start other collaborations soon to explore new areas. “I don’t know where my future research will take me. Just talking to a colleague can suddenly lead to an interesting problem,” the researcher passionately confides.