Camille Coron : la passion du calcul appliqué
Maîtresse de conférences en mathématiques à l’Université Paris-Saclay et membre du Laboratoire de mathématiques d’Orsay (LMO – Univ. Paris-Saclay, CNRS) pendant neuf années, Camille Coron occupe depuis septembre 2023 un poste de professeure junior INRAE au sein du laboratoire Mathématiques et informatique appliquées - Paris-Saclay (MIA Paris-Saclay – Univ. Paris-Saclay, AgroParisTech, INRAE). La mathématicienne s'intéresse aux probabilités et aux statistiques appliquées à la biologie, développant notamment des modèles pour la génétique des populations biparentales.
Le quotidien de Camille Coron ? Faire des calculs ! Cette passion naît chez elle en classe de seconde, grâce à son professeur de mathématiques qui lui fait découvrir le plaisir de faire des mathématiques en l’encourageant à participer au concours Kangourou, où elle excelle. Sur les conseils de ses parents, tous deux mathématiciens, Camille Coron suit, après son baccalauréat, une classe préparatoire au lycée Louis-le-Grand, à Paris, et se prépare au concours de l’ENS Paris-Saclay, qu’elle passe en 2006. Un peu lasse des mathématiques enseignées en classe préparatoire, la jeune étudiante délaisse l’agrégation pour se consacrer aux mathématiques appliquées, qu’elle découvre pendant son master 2 à l’Université Pierre et Marie Curie (aujourd’hui Sorbonne Université). « Nous faisions des mathématiques appliquées à différents domaines, notamment la biologie et l’écologie qui m’attiraient déjà à l’époque. »
C’est durant cette période que naît également son goût pour la recherche. Camille Coron choisit de s’engager dans une thèse, dirigée par Sylvie Méléard, au Centre de mathématiques appliquées (CMAP)de l'École polytechnique. Elle la soutient en 2013. Après un post-doctorat au sein de l’équipe Probabilités et statistiques du Laboratoire de mathématiques d’Orsay (LMO), elle obtient dans ce laboratoire un poste de maîtresse de conférences en 2014. À l’automne 2023, l’INRAE la recrute pour trois ans sur une chaire de professeure junior (CPJ) et elle rejoint l’équipe Statistical modelling and Learning for environnement and Life Sciences (SOLSTIS) du laboratoire Mathématiques et informatique appliquées - Paris-Saclay (MIA Paris-Saclay). « Si tout se passe bien, je deviendrai à terme directrice de recherches INRAE », se réjouit la jeune chercheuse.
Oiseaux, moustiques et qualité de l’air
Les équations de Camille Coron sont capables de modéliser tous les sujets. La mathématicienne réalise aussi de la simulation informatique, un atout pour tous ses projets. « J'ai avant tout besoin que le sujet me plaise ! De préférence, il faut qu’il soit dans les domaines de la biologie, de l’écologie ou de l’environnement. Le cœur de mon activité de recherche consiste à trouver des modèles mathématiques pour répondre à une question initiale scientifique, en biologie par exemple. J’étudie le modèle puis le confronte à une certaine réalité constatée sur cette question, en collaboration avec mes collègues biologistes. »
Ainsi, lors de son post-doctorat au LMO, Camille Coron contribue à cartographier les différentes populations d’oiseaux présents dans la Région Aquitaine, en collaboration avec Christophe Giraud. « Il s’agissait de confronter deux jeux de données obtenues très différemment pour en faire une cartographie la plus fiable possible des différentes espèces d’oiseaux. »
Dans une démarche similaire, la mathématicienne collabore avec l’INSA Rouen pour dessiner la carte précise du taux de concentration de dioxyde d'azote dans les quartiers de la ville. En combinant des mesures de concentrations réelles à des modèles physico-chimiques, elle s’attache à corriger les biais de ces modèles liés à certaines quantités ou phénomènes qu’ils négligent (variation d’altitude, d’occupation du sol, etc.) « Les particules fines étant très nocives, le but est d’alerter la population en cas de dépassement du seuil de tolérance. »
Réguler des populations de moustiques constitue un enjeu sanitaire tout aussi important dans certaines régions. Une des façons de lutter contre les espèces nuisibles se fait en lâchant une grande quantité de moustiques mâles stériles - le moustique mâle ne pique pas - de manière à multiplier les accouplements des moustiques femelles avec ces mâles. C’est la technique de l’insecte stérile (TIS). Les œufs générés n’étant pas viables, il s’ensuit une chute drastique de la population de moustiques. « Je cherche à calculer des modèles mathématiques qui modélisent ce protocole d'expérience pour trouver la meilleure façon de l'appliquer. Vaut-il mieux lâcher les moustiques mâles tous les jours ou toutes les semaines ? À quel moment et dans quels lieux va-t-on devoir recommencer ? »
Génétique des populations biparentales
Camille Coron s’intéresse aussi à la modélisation des populations biparentales, et ce, dès sa thèse. « Dans beaucoup d'espèces, un individu comporte deux parents. Son génome est donc une fonction aléatoire de leurs génomes. Si les individus sont diploïdes, c’est-à-dire si chaque gène se retrouve en deux copies chez un même individu, alors un des parents donne une de ces deux copies à son enfant et l'autre parent donne une autre copie. Lorsqu’on étudie la génétique biparentale, on s’intéresse particulièrement à ces deux copies. Il en découle une complexité très étudiée d'un point de vue biologique, mais plus rarement d'un point de vue mathématiques. »
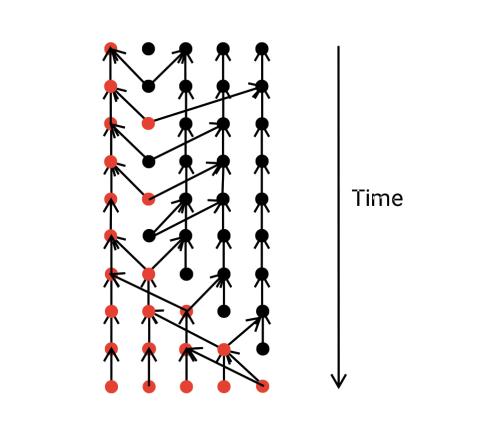
La mathématicienne s’intéresse plus précisément au cheminement d’un gène dans une population donnée et dont elle imagine de nouveaux modèles. « Je prends un gène dans le temps présent pour étudier son histoire, c’est-à-dire sa généalogie, non pas au sens courant du terme qui consiste à rechercher l’ensemble des parents dans un "arbre généalogique". Ce qui m’intéresse, c’est plutôt de partir du gène lui-même pour étudier son parcours dans le pedigree, c’est-à-dire l’ensemble des relations de parenté entre individus. »
Équilibre entre mutation et sélection
Alors que le gène ne suit qu’un seul chemin, il sera forcément possible de le rencontrer au bout d’un moment chez un individu. Il en va de même avec un autre gène. « À chaque fois que ces deux gènes seront ensemble, ils le seront pour toujours. J'aurai donc un seul ancêtre, commun à la population. » Des alternatives existent pourtant, que la mathématicienne modélise. « J’ai démontré que la moitié des individus est susceptible de contribuer à l’ensemble de la population alors que l’autre moitié ne contribue à personne. Dans ce cas, l’individu n’a aucune descendance sur un temps long. » La mathématicienne s’intéresse également aux phénomènes de mutations des gènes. « Il s’agit d’étudier l'équilibre entre la mutation et la sélection du génome dans une population donnée. Nous avons par exemple observé le phénomène d'apparition de mutants récurrents. La question revient alors à déterminer si un meilleur type de gènes se retrouve dans une proportion non négligeable de la population. »
Faites des maths !
Pour Camille Coron, sa passion pour les mathématiques demeure intacte. « Je me souviens encore du jour où j’ai obtenu mon poste de maîtresse de conférences. L’effet "whaou" a duré plusieurs mois, confie celle qui n’a jamais envisagé d’autres voies. Aujourd’hui encore, je me réveille le matin avec l’idée que le métier d’enseignante-chercheuse est génial. Nul autre métier n’offre autant de liberté : choisir sur quoi et avec qui on travaille. » C’est le premier message que l’enseignante-chercheuse délivre à ses étudiantes et étudiants, en techniques de commercialisation à l’IUT de Sceaux et auxquels elle a enseigné les mathématiques pendant neuf ans ou du master 2 Mathématiques pour les sciences du vivant de l’Université Paris-Saclay qu’elle dirige actuellement. « Faites des maths » serait son second message. « Qui se passionne pour les mathématiques trouvera forcément son bonheur car elles s’ouvrent à beaucoup d’autres disciplines et mènent à de nombreux métiers », conclut Camille Coron.

