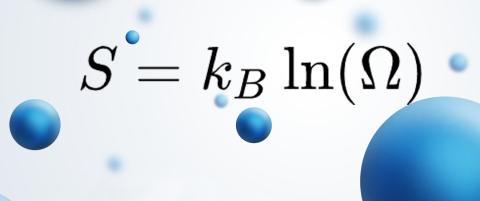
Thierry Bodineau: Coherence in randomness

Thierry Bodineau is a French National Centre for Scientific Research (CNRS) Research Director at the Alexander Grothendieck Laboratory (LAG - Univ. Paris-Saclay, CNRS, IHES) and a specialist in probability. His work focuses on statistical mechanics problems and lies at the intersection of mathematics and physics.

Thierry Bodineau decided early on to study probability, which allows him to maintain connections between his two favourite disciplines of mathematics and physics. After studying at the École normale supérieure (ENS - University-level teaching institute) Ulm, he defended his thesis on the Ising model in a disordered environment at Université Paris-Diderot (now Université Paris Cité) in 1997. He joined the CNRS as a research fellow shortly afterwards. He received his Accreditation to Supervise Research (HDR) in 2005 and returned to ENS Ulm two years later as CNRS Research Director. Between 2008 and 2009, he spent a year in the United States, first at Rutgers in New Jersey and then at the Institute for Advanced Study. In 2014, Thierry Bodineau joined the Center for Applied Mathematics at École Polytechnique (CMAP). He served as Deputy Director of the Doctoral school Jacques Hadamard before becoming Director of CMAP in 2020. In September 2022, he joined IHES - Institut des Hautes Etudes Scientifiques, the "temple of mathematics and physics".

From the random to the unchangeable

“My core activity involves finding equations for the transition from the microscopic level, where atoms display almost random behaviour, to the macroscopic level, which is governed by the immutable laws of physics," says the researcher. “We all know the example of water, which always boils and freezes at the same temperature. In a gas, the atoms interact with each other locally, and almost chaotically, and a precise analysis of their trajectories would be infinitely complex. But if we look at their average behaviour, the gas can be described simply using a few parameters such as temperature or pressure. As a probabilist, I try to mathematically justify the emergence of macroscopic order from microscopic patterns with a seemingly disordered structure."

Statistical mechanics provides mathematicians with a vast field of questions and extremely diverse microscopic models. In recent years, Thierry Bodineau has been more specifically interested in finding kinetic theory equations from molecular dynamics that evolve according to the fundamental principles of mechanics.

The Boltzmann equation

In the 1870s, Austrian physicist Ludwig Boltzmann put forward an equation that governed the evolution of a dilute gas out of equilibrium. "Imagine a very large snooker table whose balls represent the atoms of a gas. The number of these balls is huge because it corresponds to Avogadro's number, i.e. 1023," continues the researcher. “The movement of the balls is completely deterministic, just like on a snooker table; it obeys Newton's laws and we try to analyse their evolution. When we follow the trajectories of all these balls, we can, at least in theory, change the direction of time and make the balls go back to their original positions. No information has been lost." However, the Boltzmann equation, which is supposed to take this microscopic system into account, does not have this property of reversibility as it loses memory over time. "The challenge therefore lies in proving mathematically that the equation correctly describes the dynamics of snooker, even if it does not share all its properties," adds the mathematician.

Ten years of research

Oscar Lanford, an IHES professor in the 1980s, found the first mathematical proof of the link between the microscopic model and the Boltzmann equation. However, questions remain. In particular, Lanford's proof is only valid for very short periods, around the average collision time between two atoms of the gas. Thierry Bodineau has been working to simplify and extend this mathematical proof for around ten years, in collaboration with Laure Saint-Raymond, Isabelle Gallagher and Sergio Simonella. The scientists first established that Boltzmann's description remains valid for long periods and for regimes very close to equilibrium, and "that this description extends well beyond the typical behaviour of a gas because it allows the statistics of fluctuations to be quantified." This teamwork has resulted in a number of publications and earned the researcher the 2022 Sophie Germain Prize – Fondation de l’Institut de France from the French Academy of Sciences. "We are now trying to justify the Boltzmann equation over longer periods. The more we advance in this subject, the more we understand its extreme complexity, but we are making progress," assures Thierry Bodineau.